关于过n个点画出平滑曲线的数学原理

Posted on | In |

过已知的n个点如何画出平滑的曲线呢? 你会觉得很简单啊，使用贝塞尔曲线就行了，可最多只能使用三阶贝塞尔曲线，如何使两个贝塞尔曲线在连接点保持平滑呢？

贝塞尔曲线

贝塞尔曲线的数学基础是早在 1912 年就广为人知的伯恩斯坦多项式。但直到 1959 年，当时就职于雪铁龙的法国数学家 Paul de Casteljau 才开始对它进行图形化应用的尝试，并提出了一种数值稳定的 de Casteljau 算法。然而贝塞尔曲线的得名，却是由于 1962 年另一位就职于雷诺的法国工程师 Pierre Bézier 的广泛宣传。他使用这种只需要很少的控制点就能够生成复杂平滑曲线的方法，来辅助汽车车体的工业设计。

正是因为控制简便却具有极强的描述能力，贝塞尔曲线在工业设计领域迅速得到了广泛的应用。不仅如此，在计算机图形学领域，尤其是矢量图形学，贝塞尔曲线也占有重要的地位。今天我们最常见的一些矢量绘图软件，如 Flash、Illustrator、CorelDraw 等，无一例外都提供了绘制贝塞尔曲线的功能。甚至像 Photoshop 这样的位图编辑软件，也把贝塞尔曲线作为仅有的矢量绘制工具（钢笔工具）包含其中。

  1. 一阶贝塞尔曲线
    一阶曲线只有起点和终点P0和P1，就是一直线(图片和方程引用wiki，下同)
    ref wiki
    方程：
  2. 二阶贝塞尔曲线
    二阶曲线除了起点P0，终点P2，还有一个控制点P1，此时就是一个曲线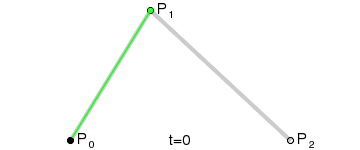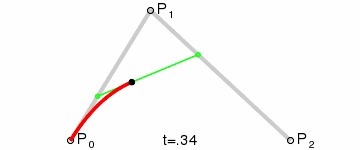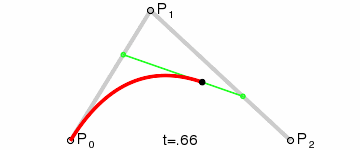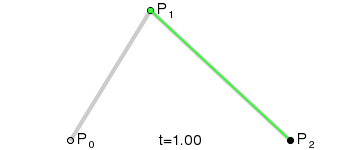


    方程:

    整理后:

    一阶导数:

    二阶导数:
  3. 三阶贝塞尔曲线
    三阶曲线除了起点P0，终点P3，还有两个控制点P1, P2，此时也是一个曲线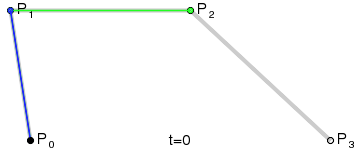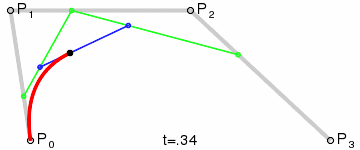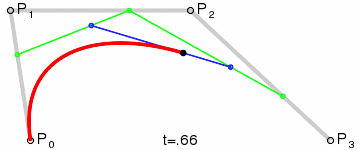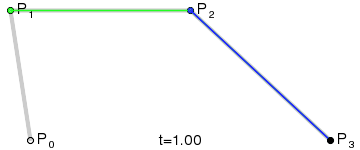


    方程:

    简化后:

    一阶导数:

    二阶导数:

何谓平滑

什么叫两个贝塞尔曲线在连接点P处保持平滑呢？从数学意义上讲，应该是曲线在P处可导，同时我们还希望P点左右两边曲线的凹凸性相同，也就是P点左右两边一阶和二阶导数相等

分析

给定n个点，我们可以取相邻两个点画一个三阶贝塞尔曲线，关键在于如何获得两个点之间的控制点，使得相邻的曲线在相邻点处的一阶和二阶导数相等；
三阶贝塞尔曲线可以表示成：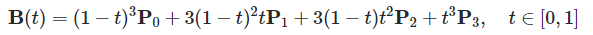

整理: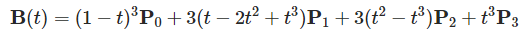

我们现在需要边界点处一阶导数相等, 一阶导数可以表示成：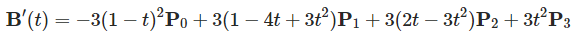

第i个曲线的起点处有方程: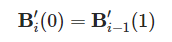

有：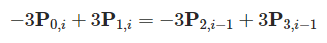

既然曲线是连续的，那么就有：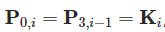

我们可以简化(1)式: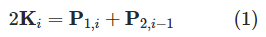

同样我们也需要二阶导数相等: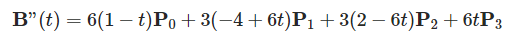

在边界处二阶导数相等：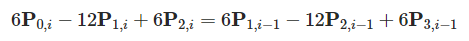

简化后等到(2)式：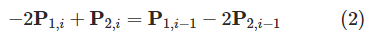

将(1)和(2)组合消去P2,i和P2,i-1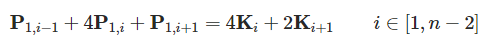

这符合三对角矩阵算法，但上面只有n-2个等式，还需要2个等式，我们可以找边界条件：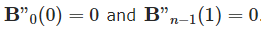

由此我们可以等到(3)和(4)：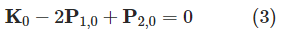


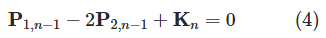
使用(1)式将(3)中消去P2,0，得到：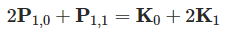

在(1)式和(2)式中，令i=n-1，带入(4)式中消去P2,n-1，得到：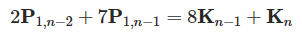

利用三对角矩阵算法可以算出P1,i，再由(1)和(4)式可以得到P2,i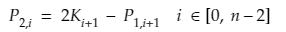

和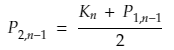

code snippet

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
private void makeCubicBezierPath(List<PointF> points, Path path) {
    float[] p1_x;
    float[] p1_y;
    float[] p2_x;
    float[] p2_y;
    float[] k_x = new float[points.size()];
    float[] k_y = new float[points.size()];
    for (int i = 0; i < points.size(); i++) {
        k_x[i] = points.get(i).x;
        k_y[i] = points.get(i).y;
    }
    p1_x = computeCoordinateForP1(k_x);
    p1_y = computeCoordinateForP1(k_y);
    p2_x = computeCoordinateForP2(k_x, p1_x);
    p2_y = computeCoordinateForP2(k_y, p1_y);

    path.reset();
    path.moveTo(points.get(0).x, points.get(0).y);

    for (int i = 0; i < points.size() - 1; i++) {
        path.cubicTo(p1_x[i], p1_y[i],
                p2_x[i], p2_y[i],
                points.get(i + 1).x, points.get(i + 1).y);
    }
}

private float[] computeCoordinateForP1(float[] k) {
    int n = k.length - 1;
    float[] a = new float[n];
    float[] b = new float[n];
    float[] c = new float[n];
    float[] d = new float[n];

    /*left most segment*/
    a[0] = 0;
    b[0] = 2;
    c[0] = 1;
    d[0] = k[0] + 2 * k[1];

    /*internal segments*/
    for (int i = 1; i < n - 1; i++) {
        a[i] = 1;
        b[i] = 4;
        c[i] = 1;
        d[i] = 4 * k[i] + 2 * k[i + 1];
    }

    /*right segment*/
    a[n - 1] = 2;
    b[n - 1] = 7;
    c[n - 1] = 0;
    d[n - 1] = 8 * k[n - 1] + k[n];

    return tdma(a, b, c, d);
}

private float[] computeCoordinateForP2(float[] k, float[] p1) {
    int n = p1.length;
    float[] p2 = new float[n];
    for (int i = 0; i < n - 1; i++) {
        p2[i] = 2 * k[i + 1] - p1[i + 1];
    }
    p2[n - 1] = 0.5f * (k[n] + p1[n - 1]);
    return p2;
}

/**
    * The tridiagonal matrix algorithm (TDMA), also known as the Thomas algorithm,
    * is a simplified form of Gaussian elimination that can be used to solve tridiagonal
    * systems of equations. A tridiagonal system for n unknowns may be written as
    * a[i]*x[i-1]+b[i]*x[i]+c[i]*x[i+1]=d[i], where a[0]=0 and c[n-1]=0.
    * <p>
    */
float[] tdma(float[] a, float[] b, float[] c, float[] d) {
    int n = d.length;
    float temp;
    c[0] /= b[0];
    d[0] /= b[0];
    for (int i = 1; i < n; i++) {
        temp = 1.0f / (b[i] - a[i] * c[i - 1]);
        c[i] *= temp;
        d[i] = (d[i] - a[i] * d[i - 1]) * temp;
    }
    float[] result = new float[n];
    result[n - 1] = d[n - 1];
    for (int i = n - 2; i >= 0; i--) {
        result[i] = d[i] - c[i] * result[i + 1];
    }
    return result;
}

reference

贝塞尔曲线扫盲
wikipedia
bezier-splines

0%